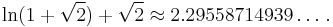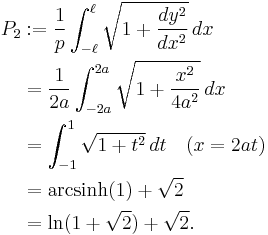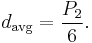Universal parabolic constant

The universal parabolic constant is a mathematical constant.

It is defined as the ratio, for any parabola, of the arc length of the parabolic segment formed by the latus rectum to the focal parameter. It is denoted P2.[1]

In the diagram, the latus rectum is pictured in blue, the parabolic segment that it forms in red and the focal parameter in green.

The value of P2 is

\ln(1 %2B \sqrt2) %2B \sqrt2 \approx 2.29558714939\dots\,.

The circle and parabola are unique among conic sections in that they have a universal constant. The analogous ratios for ellipses and hyperbolas depend on their eccentricities. This means that all circles are similar and all parabolas are similar, whereas ellipses and hyperbolas are not.

Contents

Derivation

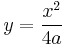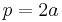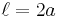Take y = \frac{x^2}{4a} as the equation of the parabola. The focal parameter is p=2a and the semilatus rectum is \ell=2a.

\begin{align} P_2 &�:= \frac{1}{p}\int_{-\ell}^\ell \sqrt{1%2B\frac{dy^2}{dx^2}}\, dx \\ & = \frac{1}{2a}\int_{-2a}^{2a}\sqrt{1%2B\frac{x^2}{4a^2}}\, dx \\ & = \int_{-1}^{1}\sqrt{1%2Bt^2}\, dt \quad (x=2at) \\ & = \operatorname{arcsinh}(1)%2B\sqrt{2}\\ & = \ln(1%2B\sqrt{2})%2B\sqrt{2}. \end{align}

Properties

P2 is a transcendental number.

Proof. Suppose that P2 is algebraic. Then 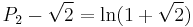\!\ P_2 - \sqrt2 = \ln(1 %2B \sqrt2) must also be algebraic. However, by the Lindemann–Weierstrass theorem, 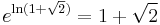\!\ e^{\ln(1%2B \sqrt2)} = 1 %2B \sqrt2 would be transcendental, which is not the case. Hence P2 is transcendental.

Since P2 is transcendental, it is also irrational.

Applications

The average distance from a point randomly selected in the unit square to its center is[2]

d_\text{avg} = {P_2 \over 6}.

References

  1. ^ Sylvester Reese and Jonathan Sondow, "Universal Parabolic Constant" from MathWorld., a Wolfram Web resource.
  2. ^ Eric W. Weisstein, "Square Point Picking" from MathWorld., a Wolfram Web resource.